
Figure: Fonctions de corrélation de l'UDLS et du CfA
Nous avons ensuite appliqué plusieurs indicateurs statistiques: fonctions de corrélation et de corrélation croisée, percolation, fonction de multiplicité, Minimal Spanning Tree, probabilité de vides.

Figure: Fonctions de corrélation de l'UDLS et du CfA
Les fonctions de corrélation respectives du CfA et de l'UDLS
(fig.![]() ) sont comparables à toutes les profondeurs.
Il y a quand même une caractéristique significative:
les échantillons plus profonds
ont des longueurs de corrélation
) sont comparables à toutes les profondeurs.
Il y a quand même une caractéristique significative:
les échantillons plus profonds
ont des longueurs de corrélation 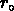 plus grandes.
On a à peu près la relation
plus grandes.
On a à peu près la relation 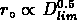 , où
, où
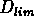 est la distance limite de l'échantillon. Ce phenomène
(voir Einasto et al., 1986; Hamilton, 1988; Davis et al., 1988;
Maurogordato & Lachièze-Rey, 1991)
pourrait signifier que ces échantillons ne sont pas encore
représentatifs de l'Univers,
ou que la corrélation des galaxies dépend de leur luminosité.
est la distance limite de l'échantillon. Ce phenomène
(voir Einasto et al., 1986; Hamilton, 1988; Davis et al., 1988;
Maurogordato & Lachièze-Rey, 1991)
pourrait signifier que ces échantillons ne sont pas encore
représentatifs de l'Univers,
ou que la corrélation des galaxies dépend de leur luminosité.
Cette similarité des fonctions de corrélation a d'autres implications. Effectivement, elle semble impliquer que les galaxies de faible brillance de surface ont la même fonction de corrélation que les autres galaxies, en désaccord avec les prédictions de certaines théories de formation biaisée de galaxies.
Nous avons pris en considération le rapport entre 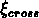 et
et
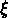 , qui doit être égal à l'unité en cas d'absence d'effets
de ségrégation (Alimi, Valls-Gabaud & Blanchard 1988; Thuan et al., 1991).
Cette statistique aussi n'a pas donné de différences significatives.
, qui doit être égal à l'unité en cas d'absence d'effets
de ségrégation (Alimi, Valls-Gabaud & Blanchard 1988; Thuan et al., 1991).
Cette statistique aussi n'a pas donné de différences significatives.
La percolation montre au contraire des différences: dans le
cas des catalogues limités à 40 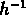 Mpc , l'UDLS percole avant le CfA:
on a
Mpc , l'UDLS percole avant le CfA:
on a 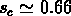 contre
contre 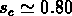 .
Le contraire se vérifie pour les échantillons limités à 60 et à 80
.
Le contraire se vérifie pour les échantillons limités à 60 et à 80
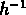 Mpc . Nous avons interprété cet effet comme une conséquence du fait que,
dans le cas de l'UDLS40 et du CfA40, les galaxies de faible brillance de
surface constituent des ponts qui facilitent la percolation.
Quant aux échantillons plus profonds, ils sont dominés par le superamas
Coma-A1367, qui est notoirement pauvre en galaxies spirales; cette structure est
moins échantillonée dans l'UDLS, qui perd plus facilement les
galaxies des premiers types, ce qui retarde la
percolation de l'UDLS60 et de l'UDLS80.
Mpc . Nous avons interprété cet effet comme une conséquence du fait que,
dans le cas de l'UDLS40 et du CfA40, les galaxies de faible brillance de
surface constituent des ponts qui facilitent la percolation.
Quant aux échantillons plus profonds, ils sont dominés par le superamas
Coma-A1367, qui est notoirement pauvre en galaxies spirales; cette structure est
moins échantillonée dans l'UDLS, qui perd plus facilement les
galaxies des premiers types, ce qui retarde la
percolation de l'UDLS60 et de l'UDLS80.
On trouve aussi des résultats intéressants dans l'analyse de la fonction de
multiplicité. Le CfA40 et UDLS40 ont des courbes 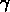 différentes
entre
différentes
entre 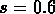 et s = 1 (je rappelle que
et s = 1 (je rappelle que 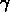 représente la
fraction de galaxies dans les systèmes riches). Les responsables de cette
différence sont 45 galaxies qui se trouvent dans l'UDLS et sont absentes
dans le CfA, et qui forment un ``pont" qui facilite le processus de
percolation. PWCS ont trouvé que les galaxies du SSRS se trouvent
dans des systèmes plus grands que les galaxies du CfA; notre
résultat montre que cela peut être une conséquence du critère de
sélection, même si la différence des structures observées peut avoir
son influence.
représente la
fraction de galaxies dans les systèmes riches). Les responsables de cette
différence sont 45 galaxies qui se trouvent dans l'UDLS et sont absentes
dans le CfA, et qui forment un ``pont" qui facilite le processus de
percolation. PWCS ont trouvé que les galaxies du SSRS se trouvent
dans des systèmes plus grands que les galaxies du CfA; notre
résultat montre que cela peut être une conséquence du critère de
sélection, même si la différence des structures observées peut avoir
son influence.
L'analyse avec le MST confirme les résultats précédents, et donne
une visualisation des différences (fig.![]() ).
).

Figure: MST pour UDLS et CfA: l'échantillon à 60 Mpc du CfA est en
réalité constitué de deux branches, qui sont vus connectés par
effet de projection
L'analyse de la distribution des vides avec le test de Ryden & Turner (1984)
montre que les sous-échantillons CfA ont des vides plus grands. En plus,
une analyse
de la probabilité de vides 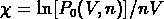 en fonction
de
en fonction
de 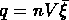 montre que les sous-échantillons CfA ont une plus grande
valeur de
montre que les sous-échantillons CfA ont une plus grande
valeur de 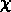 . Il faut dire que cette différence est légère
dans les échantillons limités à 40 et 80
. Il faut dire que cette différence est légère
dans les échantillons limités à 40 et 80 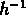 Mpc , mais qu'elle est
importante entre
le CfA60 et l'UDLS60, qui sont les moins représentatifs car ils
contiennent seulement une partie du superamas Coma-A1367, ce qui fausse la
statistique.
A nouveau ces résultats semblent nous suggérer qu'aux ordres supérieurs
(je rappelle que
Mpc , mais qu'elle est
importante entre
le CfA60 et l'UDLS60, qui sont les moins représentatifs car ils
contiennent seulement une partie du superamas Coma-A1367, ce qui fausse la
statistique.
A nouveau ces résultats semblent nous suggérer qu'aux ordres supérieurs
(je rappelle que 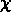 est liée aux fonctions de corrélations à tous
les ordres) les galaxies d'un catalogue limité en diamètre, sont
moins agglutinées.
Mon opinion est que l'ensemble de nos résultats peut être expliqué
de la manière suivante.
On a vu que les galaxies UDLS, dont une fraction importante est constituée de
spirales et de galaxies de faible brillance de surface,
sont plutôt disposées sur des filaments, tandis que
les galaxies CfA, dont une fraction plus grande est composée d'elliptiques,
se trouvent dans des structures plus concentrées, tel l'amas de Coma
(comme impliqué par ailleurs par la relation morphologie-densité).
Or dans un amas, qui est une concentration à 3-D,
le nombre de triplets et de systèmes multiples qui
donnent les fonctions de corrélations à 3 points et d'ordre
supérieur seront
plus nombreux que dans les filaments, qui sont des structures 1-D.
est liée aux fonctions de corrélations à tous
les ordres) les galaxies d'un catalogue limité en diamètre, sont
moins agglutinées.
Mon opinion est que l'ensemble de nos résultats peut être expliqué
de la manière suivante.
On a vu que les galaxies UDLS, dont une fraction importante est constituée de
spirales et de galaxies de faible brillance de surface,
sont plutôt disposées sur des filaments, tandis que
les galaxies CfA, dont une fraction plus grande est composée d'elliptiques,
se trouvent dans des structures plus concentrées, tel l'amas de Coma
(comme impliqué par ailleurs par la relation morphologie-densité).
Or dans un amas, qui est une concentration à 3-D,
le nombre de triplets et de systèmes multiples qui
donnent les fonctions de corrélations à 3 points et d'ordre
supérieur seront
plus nombreux que dans les filaments, qui sont des structures 1-D.
Cela peut expliquer pourquoi les fonctions de corrélation
à deux points sont comparables, tandis que les différences deviennent
sensibles (même si elles ne sont jamais très grandes: 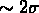 )
aux ordres supérieurs.
)
aux ordres supérieurs.