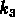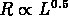 . Cette relation présente une
dispersion importante; le
. Cette relation présente une
dispersion importante; le 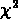 vaut en effet 2.7.
Pour les 16 amas de dispersions de vitesse connues,
nous avons trouvé une relation
vaut en effet 2.7.
Pour les 16 amas de dispersions de vitesse connues,
nous avons trouvé une relation 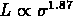 (fig.
(fig.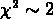 ).
).
La figure ![]() montre les 29 amas pour lesquels West et al.
ont trouvé une relation
montre les 29 amas pour lesquels West et al.
ont trouvé une relation 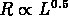 . Cette relation présente une
dispersion importante; le
. Cette relation présente une
dispersion importante; le 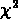 vaut en effet 2.7.
Pour les 16 amas de dispersions de vitesse connues,
nous avons trouvé une relation
vaut en effet 2.7.
Pour les 16 amas de dispersions de vitesse connues,
nous avons trouvé une relation 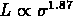 (fig.
(fig.![]() ), toujours avec une dispersion sensible (
), toujours avec une dispersion sensible (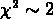 ).
).

Figure: Relation L - R pour 29 amas d'Abell (West et al., 1989)

Figure: Relation 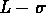 pour 16 des 29 amas d'Abell de l'échantillon
de West et al. (1989)
pour 16 des 29 amas d'Abell de l'échantillon
de West et al. (1989)
Nous avons alors recherché une relation du type
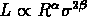 , en laissant varier les paramètres
, en laissant varier les paramètres
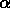 et
et 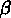 , et nous avons trouvé cette fois une relation
très peu dispersée, avec
, et nous avons trouvé cette fois une relation
très peu dispersée, avec 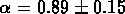 et
et 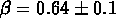 (fig.
(fig.![]() ).
).

Figure: Relation 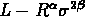 (``plan fondamental" vu de profil) pour les amas de galaxies
(``plan fondamental" vu de profil) pour les amas de galaxies
La première critique que l'on peut faire à la relation
de West et al. entre L et R est de mettre en oeuvre deux quantités qui
dépendent de la distance. En pratique, comme le décalage vers le rouge
de ces amas est très bien determiné, l'erreur sur la distance
provient essentiellement de leur mouvement propre par rapport au flux d'Hubble.
Mais on sait que ce mouvement est inférieur à 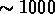 km/s, et il
n'est pas en mesure de produire une fausse corrélation entre L et
R. Par ailleurs, il pourrait affecter les paramètres de cette relation.
On peut alors définir
une brillance de surface pour les amas:
km/s, et il
n'est pas en mesure de produire une fausse corrélation entre L et
R. Par ailleurs, il pourrait affecter les paramètres de cette relation.
On peut alors définir
une brillance de surface pour les amas: 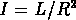 , qui ne depend plus
de la distance. On trouve alors la relation:
, qui ne depend plus
de la distance. On trouve alors la relation:

La figure ![]() montre cette relation.
montre cette relation.

Figure: Relation 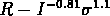 pour les amas de galaxies
pour les amas de galaxies
A partir de la relation entre L, R et 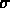 nous aurions la relation:
nous aurions la relation:
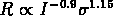 .
En plus, la relation (
.
En plus, la relation (![]() ) trouvée par Djorgovski & Davis pour
les galaxies elliptiques est tout à fait comparable.
) trouvée par Djorgovski & Davis pour
les galaxies elliptiques est tout à fait comparable.
La figure ![]() montre les amas globulaires,
les galaxies elliptiques et les amas de galaxies dans le
plan
montre les amas globulaires,
les galaxies elliptiques et les amas de galaxies dans le
plan 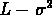 .
.

Figure: Relation 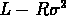 suivant la classe d'objets:
amas globulaires, galaxies elliptiques naines, galaxies elliptiques, et
amas de galaxies
suivant la classe d'objets:
amas globulaires, galaxies elliptiques naines, galaxies elliptiques, et
amas de galaxies
Il est évident qu'on a des plans différents pour chaque type
d'objets, mais de pentes comparables,
et que l'écart entre ces plans dépend du rapport 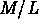 .
On peut aussi utiliser les variables définies par Bender et al. (1992).
On remplace
.
On peut aussi utiliser les variables définies par Bender et al. (1992).
On remplace 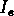 par
par
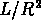 et l'on écrit donc les équations suivantes:
et l'on écrit donc les équations suivantes:
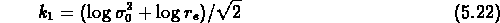
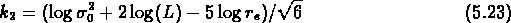
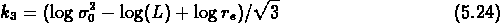
La figure ![]() montre
le plan fondamental vu de profil
(
montre
le plan fondamental vu de profil
(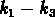 ) et vu de face (
) et vu de face (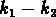 ).
).

Figure: Plan fondamental exprimé avec les variables 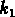 ,
, 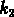 ,
,