



Next: Conclusions
Up: Modèles de la
Previous: Distribution Negative Binomiale
La description complète d'une distribution de N objets est donnée
par la connaissance des fonctions de corrélation à n points
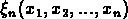 , pour tous les n.
Les observations nous disent que
la fonction de corrélation à deux points
, pour tous les n.
Les observations nous disent que
la fonction de corrélation à deux points 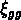 des galaxies
est une loi de puissance de pente
des galaxies
est une loi de puissance de pente 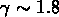 .
Groth et Peebles (1977) ont calculé la fonction de corrélation à
trois points des galaxies du catalogue de Zwicky, et ont trouvé
la relation
.
Groth et Peebles (1977) ont calculé la fonction de corrélation à
trois points des galaxies du catalogue de Zwicky, et ont trouvé
la relation
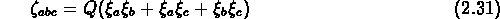
où 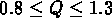 ,
et une relation analogue a été trouvé pour la fonction de corrélation
à quatre points (Sharp, Bonometto, Lucchin, 1984).
Ces résultats ont suggeré une généralisation
à tous les ordres (Fry 1984, 1986; Schaeffer 1984, 1987):
on suppose donc que
les fonctions de corrélation à N points peuvent être decomposées
en un produit de N-1 fonctions de corrélation à deux points.
,
et une relation analogue a été trouvé pour la fonction de corrélation
à quatre points (Sharp, Bonometto, Lucchin, 1984).
Ces résultats ont suggeré une généralisation
à tous les ordres (Fry 1984, 1986; Schaeffer 1984, 1987):
on suppose donc que
les fonctions de corrélation à N points peuvent être decomposées
en un produit de N-1 fonctions de corrélation à deux points.
La formulation la plus générale a été donneé par
Balian & Schaeffer (1989a), qui ont défini les modèles
invariants d'échelle:
ces modèles reproduisent bien
les observations. Ils sont définis par la relation:
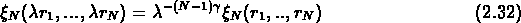
Les vieux modèles factorisés, du type de ceux de
Fry (1984) ou Schaeffer (1984)
sont des cas particuliers de ces modèles.
Pour une distribution poissonienne on a évidemment

et l'on peut écrire pour une distribution en général

Les modèles à invariance d'échelle impliquent que
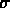 doit dépendre seulement de la variable
doit dépendre seulement de la variable 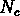 ,
définie comme
,
définie comme

où
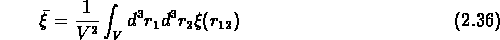
On peut aussi écrire les fluctuations des comptages en fonction de
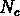 :
:
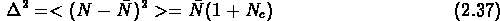
Donc 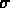 ne dépend pas séparemment du volume V, ou de la
densité n, ou des corrélations.
ne dépend pas séparemment du volume V, ou de la
densité n, ou des corrélations.
En plus, Balian & Schaeffer (1989a) ont trouvé que, pour
valeurs de 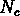 plus grandes que l'unité, on doit avoir
un comportement asymptotique en loi de puissance de
plus grandes que l'unité, on doit avoir
un comportement asymptotique en loi de puissance de
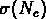 :
: 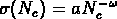 .
.
Les données pour les galaxies montrent cette loi:
par exemple, analysant le catalogue SSRS (da Costa et al., 1988)
Maurogordato, Schaeffer et da Costa
(1992) ont trouvé 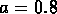 et
et 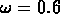 , et il y a des
indications que les amas aussi suivent la même loi
(Cappi & Maurogordato, 1991; voir chapitre 6).
, et il y a des
indications que les amas aussi suivent la même loi
(Cappi & Maurogordato, 1991; voir chapitre 6).
L'échelle 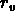 à laquelle
à laquelle 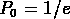 joue un rôle important.
Dans le cas d'une distribution non-corrélée,
joue un rôle important.
Dans le cas d'une distribution non-corrélée,
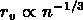 correspond à la distance inter-particule moyenne.
Naturellement, le discours peut être géneralisé aux comptages,
c'est à dire à la probabilité de trouver N objets dans un
volume donné.
Si la probabilité de vides donne une information
globale sur les fonctions de corrélations à tous les ordres, les
probabilités
correspond à la distance inter-particule moyenne.
Naturellement, le discours peut être géneralisé aux comptages,
c'est à dire à la probabilité de trouver N objets dans un
volume donné.
Si la probabilité de vides donne une information
globale sur les fonctions de corrélations à tous les ordres, les
probabilités 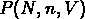 de trouver N objets dans un volume V
donnerons une information complète sur notre distribution.
Dans notre cas, l'hypothèse d'invariance d'échelle nous permet,
comme pour la
de trouver N objets dans un volume V
donnerons une information complète sur notre distribution.
Dans notre cas, l'hypothèse d'invariance d'échelle nous permet,
comme pour la 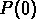 , de faire des prévisions sur le comportement
des
, de faire des prévisions sur le comportement
des 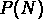 .
.
Une autre échelle importante est la clustering length 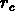 ,
où
,
où 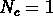 .
. 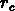 correspond physiquement à la distance
intergalactique typique dans un amas, et constitue une mesure
des propriétés locales de la distribution de galaxies.
Pour ce fait,
correspond physiquement à la distance
intergalactique typique dans un amas, et constitue une mesure
des propriétés locales de la distribution de galaxies.
Pour ce fait, 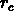 ne peut pas dépendre de la profondeur de
l'échantillon, contrairement à la longueur de corrélation
ne peut pas dépendre de la profondeur de
l'échantillon, contrairement à la longueur de corrélation
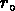 .
.
Dans le régime non-linéaire, Balian & Schaeffer (1989a) ont montré
qu'aux petites échelles ( ) et
) et 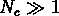 ,
,
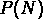 est une mesure de l'amplitude de la fonction de
corrélation d'ordre N.
A des échelles plus grandes, on a
est une mesure de l'amplitude de la fonction de
corrélation d'ordre N.
A des échelles plus grandes, on a
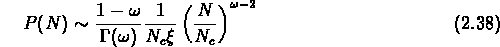
avec une coupure inférieure pour 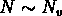 (
(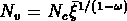 ) et une coupure
supérieure pour
) et une coupure
supérieure pour 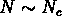 .
.
Dans les deux régions extrèmes on a des loi d'échelle.
Pour 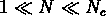 , la loi est de la forme
, la loi est de la forme
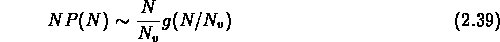
et pour  ,
,  ,
, 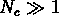 , il y a la relation
, il y a la relation
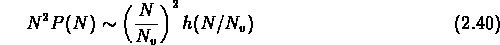
c'est à dire que les 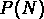 dépendent dans les deux cas
respectivement de
dépendent dans les deux cas
respectivement de 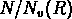 et
et 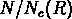 , et ils ne dépendent
pas séparémment de N ou R.
Ceci découle de la relation (
, et ils ne dépendent
pas séparémment de N ou R.
Ceci découle de la relation ( ).
).




Next: Conclusions
Up: Modèles de la
Previous: Distribution Negative Binomiale
alberto cappi
Wed Feb 5 10:43:08 MET 1997
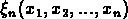 , pour tous les n.
Les observations nous disent que
la fonction de corrélation à deux points
, pour tous les n.
Les observations nous disent que
la fonction de corrélation à deux points 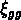 des galaxies
est une loi de puissance de pente
des galaxies
est une loi de puissance de pente 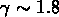 .
Groth et Peebles (1977) ont calculé la fonction de corrélation à
trois points des galaxies du catalogue de Zwicky, et ont trouvé
la relation
.
Groth et Peebles (1977) ont calculé la fonction de corrélation à
trois points des galaxies du catalogue de Zwicky, et ont trouvé
la relation
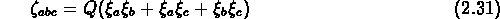
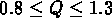 ,
et une relation analogue a été trouvé pour la fonction de corrélation
à quatre points (Sharp, Bonometto, Lucchin, 1984).
Ces résultats ont suggeré une généralisation
à tous les ordres (Fry 1984, 1986; Schaeffer 1984, 1987):
on suppose donc que
les fonctions de corrélation à N points peuvent être decomposées
en un produit de N-1 fonctions de corrélation à deux points.
,
et une relation analogue a été trouvé pour la fonction de corrélation
à quatre points (Sharp, Bonometto, Lucchin, 1984).
Ces résultats ont suggeré une généralisation
à tous les ordres (Fry 1984, 1986; Schaeffer 1984, 1987):
on suppose donc que
les fonctions de corrélation à N points peuvent être decomposées
en un produit de N-1 fonctions de corrélation à deux points.
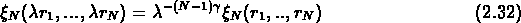


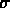 doit dépendre seulement de la variable
doit dépendre seulement de la variable 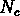 ,
définie comme
,
définie comme

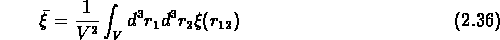
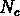 :
:
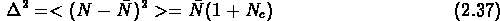
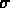 ne dépend pas séparemment du volume V, ou de la
densité n, ou des corrélations.
ne dépend pas séparemment du volume V, ou de la
densité n, ou des corrélations.
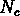 plus grandes que l'unité, on doit avoir
un comportement asymptotique en loi de puissance de
plus grandes que l'unité, on doit avoir
un comportement asymptotique en loi de puissance de
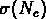 :
: 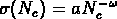 .
.
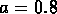 et
et 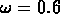 , et il y a des
indications que les amas aussi suivent la même loi
(Cappi & Maurogordato, 1991; voir chapitre 6).
, et il y a des
indications que les amas aussi suivent la même loi
(Cappi & Maurogordato, 1991; voir chapitre 6).
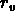 à laquelle
à laquelle 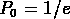 joue un rôle important.
Dans le cas d'une distribution non-corrélée,
joue un rôle important.
Dans le cas d'une distribution non-corrélée,
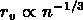 correspond à la distance inter-particule moyenne.
Naturellement, le discours peut être géneralisé aux comptages,
c'est à dire à la probabilité de trouver N objets dans un
volume donné.
Si la probabilité de vides
correspond à la distance inter-particule moyenne.
Naturellement, le discours peut être géneralisé aux comptages,
c'est à dire à la probabilité de trouver N objets dans un
volume donné.
Si la probabilité de vides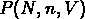 de trouver N objets dans un volume V
donnerons une information complète sur notre distribution.
Dans notre cas, l'hypothèse d'invariance d'échelle
de trouver N objets dans un volume V
donnerons une information complète sur notre distribution.
Dans notre cas, l'hypothèse d'invariance d'échelle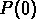 , de faire des prévisions sur le comportement
des
, de faire des prévisions sur le comportement
des 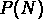 .
.
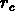 ,
où
,
où 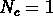 .
. 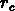 correspond physiquement à la distance
intergalactique typique dans un amas, et constitue une mesure
des propriétés locales de la distribution de galaxies.
Pour ce fait,
correspond physiquement à la distance
intergalactique typique dans un amas, et constitue une mesure
des propriétés locales de la distribution de galaxies.
Pour ce fait, 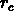 ne peut pas dépendre de la profondeur de
l'échantillon, contrairement à la longueur de corrélation
ne peut pas dépendre de la profondeur de
l'échantillon, contrairement à la longueur de corrélation
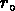 .
.
 ) et
) et 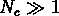 ,
,
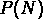 est une mesure de l'amplitude de la fonction de
corrélation d'ordre N.
A des échelles plus grandes, on a
est une mesure de l'amplitude de la fonction de
corrélation d'ordre N.
A des échelles plus grandes, on a
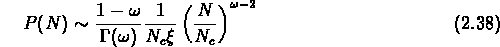
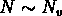 (
(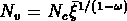 ) et une coupure
supérieure pour
) et une coupure
supérieure pour 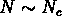 .
.
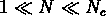 , la loi est de la forme
, la loi est de la forme
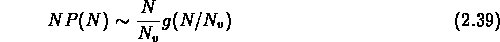
 ,
,  ,
, 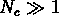 , il y a la relation
, il y a la relation
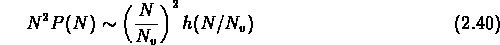
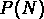 dépendent dans les deux cas
respectivement de
dépendent dans les deux cas
respectivement de 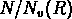 et
et 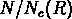 , et ils ne dépendent
pas séparémment de N ou R.
Ceci découle de la relation (
, et ils ne dépendent
pas séparémment de N ou R.
Ceci découle de la relation (