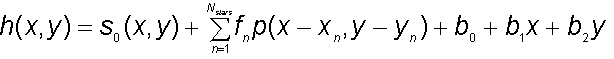

The fitting technique treats the PSF as a template which may be scaled and translated. A sub-image centered on the star of interest is extracted and approximated with the model
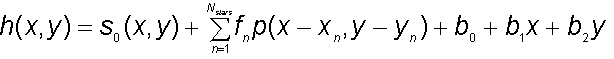
where s0 is the fixed contribution of known stars outside the sub-image support, Nstars is the number of point sources within the sub-image, xn, yn, fn are the position and flux of the n-th source, p(x,y) is the PSF and b0, b1, b2 are the coefficients of a slanting plane representing the local background.
The optimization is performed with an iterative Newton-Gauss technique, which requires the computation of the model derivatives. For this purpose the Fourier shift theorem is applied to the PSF:
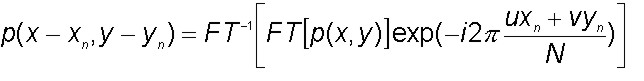
where FT is the discrete Fourier transform, N is the sub-image size and u, v are spatial frequencies. The derivative with respect to xn is
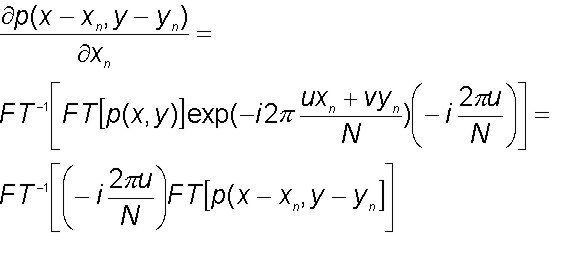
and requires the interpolation of the PSF array to compute p(x-xn, y-yn ).A similar technique has been described by J.-P. Véran and F. Rigaut (Proc.SPIE 3353,426,1998).
Many algorithms may be applied to perform the required PSF Shift. An example is the cubic convolution interpolation implemented in the IDL function Interpolate, which approaches very close the optimal "sinc " interpolation with well-sampled data. We are also investigating the accuracy achievable on marginally under-sampled (e.g. HST) images.

[Home|Authors |Presentation|Analysis |Fitting|Applications| IDL code]